在之前的教程中,我们已经学习了无源滤波器,包括无源高通 RC 滤波器和无源低通 RC 滤波器。在本教程中,我们将学习有源滤波器,特别是有源高通滤波器。
顾名思义,高通滤波器仅允许信号中的高频成分通过,同时限制低频成分。名称中的“有源”部分表明,在设计滤波器时使用了有源元件,如晶体管、运算放大器等。
如果您需要了解有源低通滤波器的相关信息,请查看这篇教程:有源低通滤波器。
高通滤波器允许高于截止频率的频率通过,并衰减低于截止频率的频率。在某些情况下,这种滤波器也被称为“低切”滤波器或“低频削减”滤波器。衰减的程度或通带范围将取决于滤波器的设计参数。
有源滤波器的通带增益大于单位增益。有源高通滤波器的工作原理与无源高通滤波器相同,��但主要区别在于有源高通滤波器使用了运算放大器,它提供了输出信号的放大和增益控制。
高通滤波器的理想特性如下图所示。

我们知道,高通滤波器将允许从截止频率点到“无穷大”频率的频率通过,而“无穷大”在实际应用中是不存在的。与无源高通滤波器不同,在这种有源高通滤波器中,最大频率响应受到运算放大器开环特性的限制。
有源高通滤波器电路
将无源 RC 高通滤波器电路连接到运算放大器的反相或同相端,即可得到一阶有源高通滤波器。连接到单位增益运算放大器同相端的无源 RC 高通滤波器电路如下图所示。

增益 Amax=1,截止频率 fc=2πRC1
高电压增益的有源高通滤波器
其工作原理与无源高通滤波器相同,但输入信号在输出时被放大器放大。放大程度取决于放大器的增益。
通带增益的幅度等于 1+R2R3,其中 R3 是反馈电阻(单位:欧姆), R2 是输入电阻。具有放大的有源高通滤波器电路如下图所示。

有源高通滤波器的电压增益
电压增益 Av=Amax1+(f/fc)2f/fc
其中:
- f = 工作频率
- fc = 截止频率
- Amax = 滤波器的通带增益 = 1+R2R3
在低频时,即工作频率低于截止频率时,滤波器的电压增益小于通带增益 Amax。在高频时,即工作频率高于截止频率时,滤波器的电压增益等于通带增益。
如果工作频率等于截止频率,则滤波器的电压增益等于 0.707Amax。
电压增益(dB)
电压增益的幅度通常以分贝(dB)表示:
Av(dB)=20log10(VinVout)
−3 dB=20log10(0.707×VinVout)
截止频率 fc 分隔了通带和阻带,可以用以下公式计算:
fc=2πRC1
有源高通滤波器的相位偏移与无源滤波器相同。在截止频率 fc 时相位偏移为 +45°,该相位偏移值为:
ϕ=tan−1(2πfcRC1)
有源高通滤波器的频率响应
与放大器开环增益相关的频率响应曲线如下图所示。
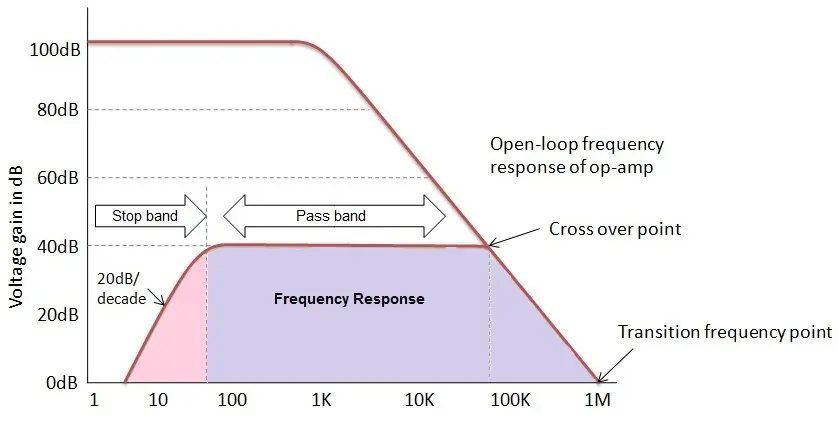
在有源高通滤波器的频率响应中,最大通带频率受到运算放大器带宽或开环特性的限制。由于这一限制,有源高通滤波器的响应将类似于宽带滤波器的响应。
通过使用基于运算放大器的有源高通滤波器,我们可以利用低容差电阻和电容实现高精度。
使用反相运算放大器的有源高通滤波器
我们知道,有源高通滤波器可以通过使用运算放大器的反相端或同相端来设计。到目前为止,我们已经看到了同相有源高通滤波器的电路和响应曲线。现在让我们看看使用反相运算放大器的有源高通滤波器。

基于拉普拉斯变换的增益推导
考虑以下反相放大器电路。

输入阻抗 Z1=sC11
其中 s = 拉普拉斯变量, C1 = 电容

流经电路的电流为 I1、 I2 和 Iin,
其中 I1=I2,且 Iin=0
Z1Vin=−R1Vout
VinVout=−Z1R1=−sC11R1=−sR1C1=增益
有源高通滤波器示例
假设截止频率值为 10 kHz,通带增益 Amax 为 1.5,电容值为 0.02 µF。
截止频率公式为:
fc=2πRC1
重新排列该公式可得:
R=2πfcC1
代入截止频率 10 kHz 和电容 0.02 µF 的值:
R=2π×10000×0.02×10−61≈795.77Ω
滤波器的通带增益为:
Amax=1+R2R3=1.5
R3=0.5R2
假设 R2 为 10 kΩ,则 R3 为 5 kΩ。
我们可以按以下方式计算滤波器的增益:
高通滤波器的电压增益:
VinVout=Amax×1+(f/fc)2f/fc
Av(dB)=20log10(VinVout)
使用该公式,我们可以为一系列频率值(假设为 10 Hz 到 100 kHz)计算响应,以便绘制滤波器的响应曲线。

波德图
为了分析电路的频率响应,我们使用波德图。波德图本质上是线性、时变系统的传递函数与频率的关系图。该图以对数频率轴绘制,主要包含两个部分:幅值图和相位图。
幅值图用于表示频率响应的幅度,即增益;而相位图用于表示频率变化的响应。
根据上述表格中的值,绘制的频率响应波德图如下:

根据计算结果,在频率为 10 Hz 时,滤波器的增益为 -56.48 dB。当频率增加到 100 Hz 时,增益为 -36.48 dB;在频率为 500 Hz 时,滤波器的增益为 -22.51 dB。
在频率为 1000 Hz 时,增益为 -16.52 dB。由此可以得出,随着频率的增加,滤波器的增益以 20 dB/十年的速率增加。
直到截止频率 10 kHz 为止,滤波器的增益不断增加,但在截止频率之后,增益达到最大值并保持恒定。
二阶高通滤波器
二阶有源滤波器的频率响应与二阶有源低通滤波器的响应完全相反,因为这种滤波器会衰减截止频率以下的电压。二阶滤波器的传递函数如下:
Vin(s)Vout(s)=−s2+(Qω0)s+ω02Ks2
其中 K=R2R1 且 ω0=CR1。
这�是二阶高通滤波器的一般形式。
二阶有源高通滤波器电路
二阶有源滤波器的设计过程与一阶滤波器相同,因为唯一的区别在于滚降特性。如果一阶有源高通滤波器的滚降为 20 dB/十年,则二阶滤波器的滚降为 40 dB/十年。
这意味着二阶滤波器的滚降是一阶滤波器的两倍。二阶滤波器的电路如下图所示:

滤波器的增益为 1+R2R1,截止频率的公式为:
fc=2πR3R4C1C21
二阶有源高通滤波器示例
让我们设计一个截止频率为 4 kHz 的滤波器,其阻带的延迟率为 40 dB/十年。由于阻带的延迟率为 40 dB/十年,我们可以明确这是一个二阶滤波器。
假设电容值为 C1=C2=C=0.02 µF。
截止频率的公式为:
R=2πfcC1
重新排列该公式可得:
R=2πfcC1
将截止频率 4 kHz 和电容 0.02 µF 的值代入:
R=2π×4000×0.02×10−61≈1.989 kΩ=2 kΩ
假设滤波器的增益为 1+R2R1=2。
R2R1=1
R1=R2
因此,我们可以取 R1=R2=10 kΩ。
得到的滤波器如下图所示:

高阶高通滤波器
通过将一阶滤波器与二阶滤波器级联,我们可以得到三阶滤波器。当我们级联两个二阶滤波器时,可以得到四阶滤波器。通过这种方式,利用一阶和二阶滤波器,我们可以得到更高阶的滤波器。
随着滤波器阶数的增加,实际阻带与理论阻带之间的差异会增加。但高阶滤波器的总增益是相等的,因为我们已经看到,决定频率响应值的电阻和电容是相同的。
这种级联顺序如下图所示:
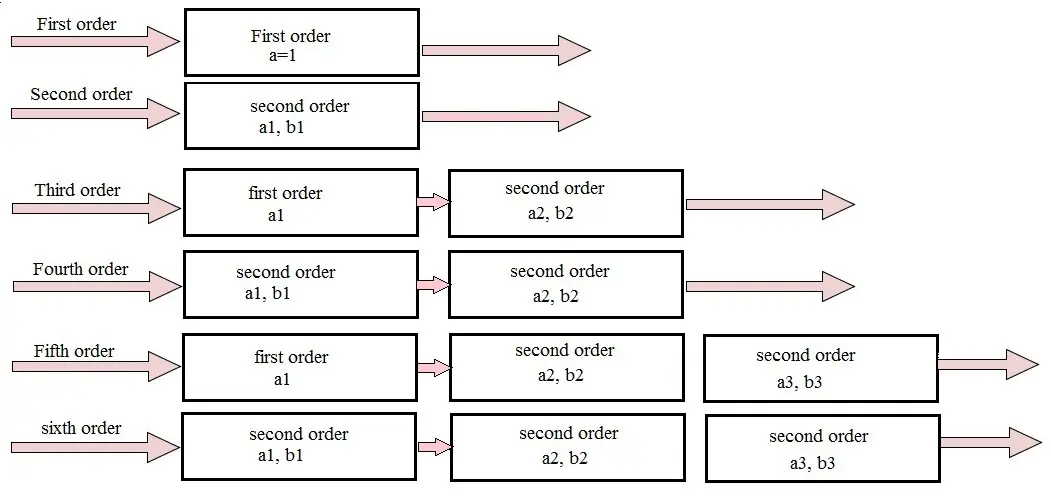
有源高通滤波器的应用
- 在扬声器中用于降低低电平噪声。
- 在音频应用中消除低频噪声(隆隆声失真),因此也被称为高频提升滤波器。
- 在音频放大器中用于放大高频信号。
- 在均衡器中也有应用。

